Számítógépes időjárás-előrejelzés rövid története
Bármilyen meglepő is laikus szemmel, az időjárás alakulása jó közelítéssel leírható fizikai törvények segítségével (a folyadék-dinamikában használt Navier-Stokes egyenletekkel, a termodinamika első főtételével, valamint az anyagmegmaradás törvényével). Az 1800-as évek közepe óta foglalkoztatta a kérdés a meteorológusokat, hogy vajon a légköri folyamatokat irányító legfontosabb fizikai törvényeket lehetséges-e matematikai formába önteni, majd azokat megoldva számszerű időjárás előrejelzést készíteni. Az időjárás alakulását leíró fizikai-matematikai egyenletrendszert Lewis Frey Richardson brit tudós foglalta össze először az 1922-ben írt „Weather prediction by numerical processes” című könyvében. Az egyenletrendszer megoldása azonban csak 28 évvel később, a számítógépek megjelenésével vált lehetővé. Nevezetesen, többek között Neumann János magyar származású matematikus részvételével készült el az első számszerű időjárás-előrejelzés 1950-ben az USA-ban az amerikai hadsereg számára fejlesztett ENIAC (Electronic Numerical Integrator And Computer) számítógépen. További öt évnek kellett eltelnie ahhoz, hogy az első operatív számítógépes előrejelzés elkészüljön Svédországban. Az 1950-es évek óta jelentős fejlődésen ment keresztül mind a számítástechnika mind az ebből profitáló meteorológia tudománya, mígnem napjainkra a számítógépes szimulációk (időjárás előrejelző modellek) nélkülözhetetlen szereplőkké váltak a napi előrejelzési gyakorlatban. Ez azt jelenti, hogy a mai meteorológiai szolgálatok mind hozzáférnek valamely számítógépes időjárás-előrejelző modell eredményeihez, illetve sok esetben saját fejlesztésű modelleket is futtatnak a számukra legérdekesebb földrajzi területre.
Nagyfelbontású időjárás-előrejelző modellek futtatása és fejlesztése
Az OMSZ középtávú előrejelzéseit (7-10 nap) főként az ECMWF (European Centre for Medium Range Weather Forecasts) által fejlesztett globális modell eredményeire alapozza, azonban a rövid távú (6-48 óra), nagy térbeli részletességgel kiadott prognózisait helyben futtatott, nagy felbontású regionális modellekre (ALADIN, AROME) támaszkodva készíti el. Ezeknek a modelleknek a fejlesztésében az OMSZ 1992 óta vesz részt az ALADIN és LACE nemzetközi együttműködések (hivatkozások) keretében. Ezek az együttműködések teszik lehetővé, hogy az OMSZ hozzáférjen a fent említett regionális modellek forráskódjához, illetve azokat saját igényei szerint fejlessze. Az együttműködő partnerek bármelyike beépítheti saját fejlesztéseit a modell egy újabb változatába, amely ezáltal minden más partner számára elérhetővé válik. Ez a konstrukció biztosítja a modell forráskódjának fejlődését és ezen keresztül a nagy felbontású előrejelzések beválásának hosszú távú javulását. Az OMSZ saját modell fejlesztései jelentős hozzáadott értéket képviselnek a Magyarországra készített célprognózisok előállításában, hiszen ezek teszik lehetővé, hogy a Kárpát-medencére jellemző regionális időjárást a lehető legjobban előrejelezzük. A saját modell fejlesztések legfontosabb előnyeit az alábbi listában foglalhatjuk össze:
- Szabadon megválaszthatjuk a földrajzi területet, amelyre az előrejelzéseket készíteni kívánjuk, illetve az előrejelzések futtatásának gyakoriságát;
- Szabadon változtathatjuk a modell rácshálózatának sűrűségét (horizontális és vertikális felbontás);
- A célterületre jellemző fizikai folyamatok figyelembevételére nagyobb hangsúlyt fektethetünk;
- A modell kiindulási feltételeiben nagy felbontású légköri megfigyeléseket (felszíni, radar, GPS és repülőgépes megfigyelések) vehetünk figyelembe, amelyek elengedhetetlenek a Magyarország térségében kialakuló regionális és lokális időjárási folyamatok előrejelzéséhez.
A korlátos tartományú modellek által adott előrejelzések széles körben alkalmazhatók. A legfontosabb alkalmazási területek a következők:
- Veszélyjelzés (szélsőséges időjárási események előrejelzése);
- Szennyezőanyag terjedés (szmog, illetve vulkáni hamu terjedés előrejelzése);
- Repülés (látástávolság, szél, csapadék előrejelzése repülőterek közelében);
- Útmeteorológia (veszélyes útviszonyok előrejelzése);
- Hidrológia (csapadék előrejelzés, lefolyás-, illetve árvíz-modellek számára);
- Szélenergia becslés (szélerőművek termelésének becslése szélelőrejelzések alapján);
- Hőenergia igény becslése (hőerőművek termelésének optimalizálása a várható hőmérséklet függvényében);
- Környezeti hatástanulmányok (pl. egy esetleges új paksi atomerőmű blokk telepítése milyen környezeti hatásokkal járna);
- Oktatás (hallgatók képzése a numerikus előrejelzés témakörében).
Numerikus modell előrejelzések alkalmazási területei
OMSZ-ban végzett numerikus előrejelzéshez kapcsolódó tevékenységek, fejlesztések
- Az ALADIN és AROME modellek lokális változatának operatív futtatása (ALADIN/HU) a Szolgálatnál. Az operatív modell futások eredményei nap mint nap felhasználásra kerülnek a médiában megjelenő, illetve az egyéb felhasználók számára (repülés, energia szektor, stb.) kiadott előrejelzések elkészítésekor.
|
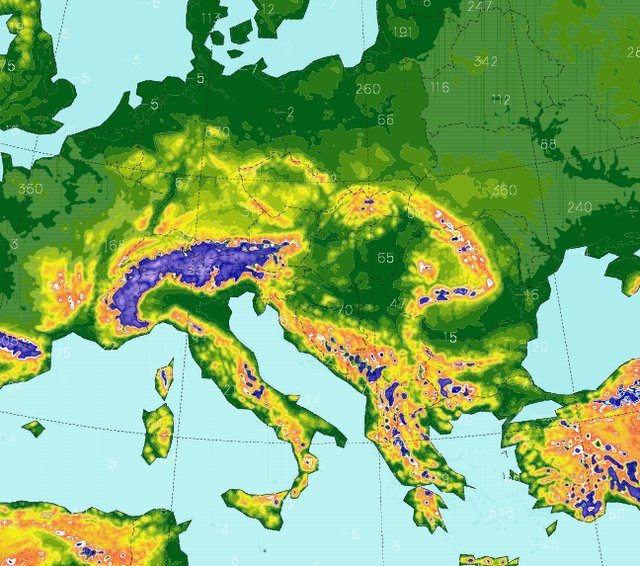
8 km-es felbontású ALADIN modell tartománya |
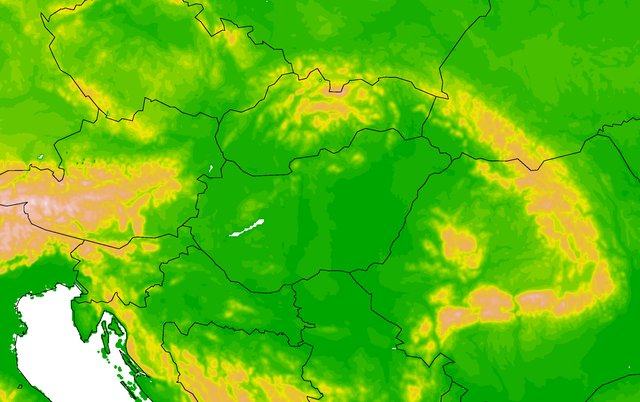
2.5 km-es felbontású AROME modell tartománya |
- Az ALADIN és AROME modellek adatasszimilációs rendszerének fejlesztése, amely a megfelelő kezdeti feltételeket állítja elő a numerikus előrejelzésekhez.
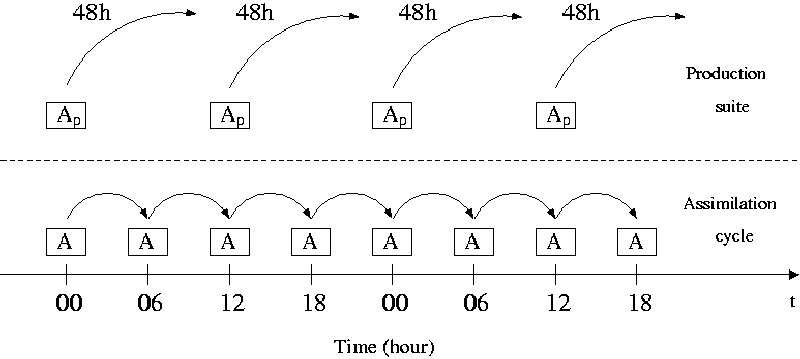
ALADIN modell adatasszimilációs ciklusa
- Az ALADIN és AROME modellek fizikai parametrizációinak fejlesztése, amely biztosítja a légkörben fontos szerepet játszó fizikai folyamatok (sugárzás, turbulencia, mikrofizika, stb.) minél pontosabb figyelembevételét.
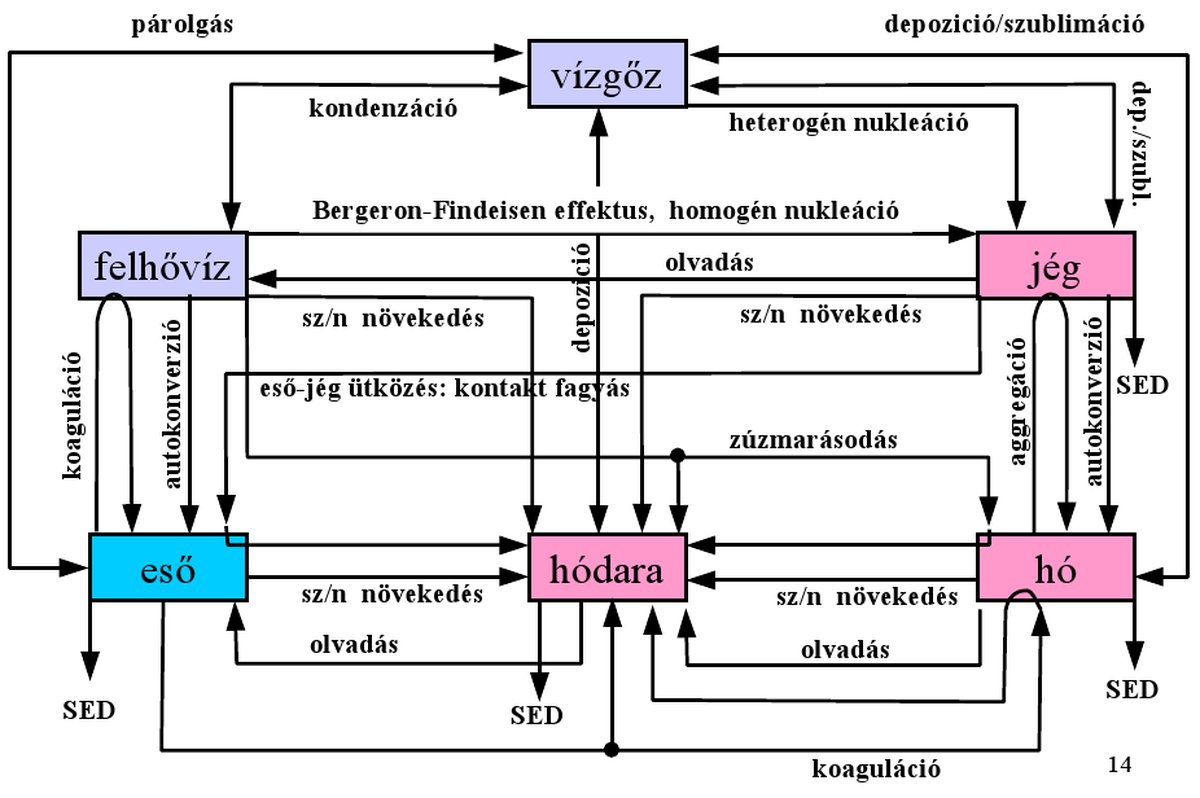
AROME modellben parametrizált mikrofizikai folyamatok
- Az ALADIN modellen alapuló rövidtávú ensemble előrejelzési módszerek (LAMEPS) fejlesztése. A LAMEPS kutatások célja a szélsőséges (például nagy csapadékok, illetve heves szélviharok) időjárási jelenségek valószínűségi alapú rövidtávú előrejelzése, azaz egy várható érték megbecslése mellett információ szolgáltatása az aktuális előrejelzésben rejlő bizonytalanság mértékéről.
A valószínűségi előrejelézések kapcsán gyakran emlegetett Lorenz attraktor
OMSZ: 2013. április 9.